G(V,E)
V:정점(vertex)
E :간선(edge)

무방향그래프의 정점쌍 {v1,v2} - 순서가 상관이 없음.
방향그래프의 간선 순서쌍 (v1,v2) - 순서가 있음 v1 ->v2
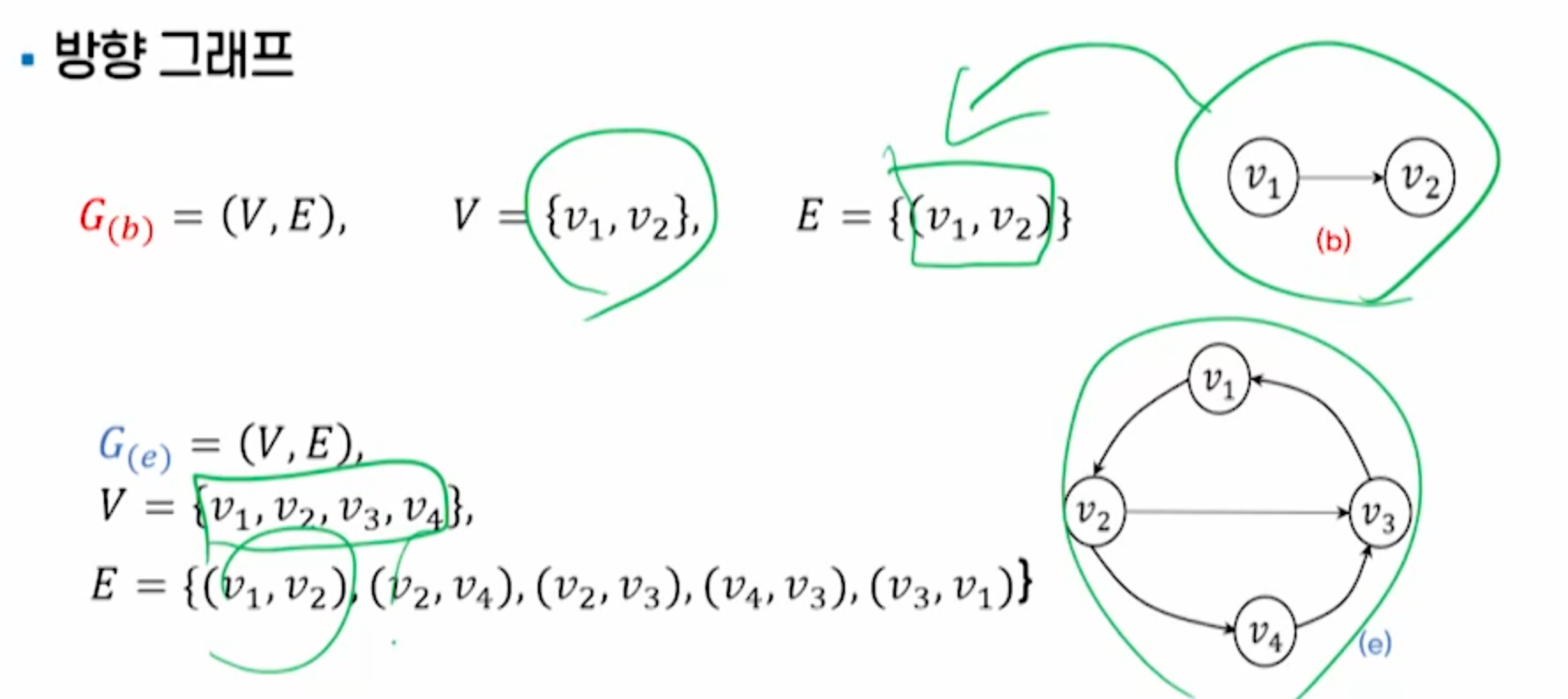
경로 길이 : 경로에 있는 간선의 수
단순 경로 : 경로상에 있는 모든 정점이 서로 다른 경로
기본 경로: 경로상에 있는 모든 간선이 서로 다른 경로 ( 자기자신으로 되돌아오는것도 경로로 봄)
사이클: 출발점과 도착점이 동일한 단순경로
무방향그래프 차수: 정점에 연결된간선들의 개수
방향그래프 차수: 진출차수와 진입차수의 합
루프: 간선의 시작점과 끝점이 같은 정점의 길이가 1인 경로 - 사이클에 포함이 됨
DAG: 방향이있는 무사이클그 래프

그래프 탐색
깊이우선탐색DFS
-스택을 사용하여 가장 최근에 선택의 지점에 있던 정점을 찾아냄
너비우선탐색 BFS
-인접 정점을 모두 방문하기 때문에 큐를 사용 함
최소비용 신장트리 (최소 신장 트리)
트리: 사이클이 없는 단순 그래프
신장트리 : 그래프G의 모든 정점과 간선의 일부를 포함하는 트리
- 주어진 그래프의 정점을 모두 포함함
- n-1개의 간선으로 구성한 그래프
G의 최소부분그래프 : 그래프G의 부분 그래프중에서 간선의 수가 가장 작은것
최소비용신장트리 : 가중치그래프G의 가중치가 작은 간선을 선택하여 구성된 신장트리
교재의 최소비용 신장트리 알고리즘은 항상 최저 비용인 신장트리의 구축을 보장하지는 않는다ㄴ.

cycle이 있는것은 신장트리가 아니다.
탐색 신장트리
깊이우선 신장트리
너비우선신장트리
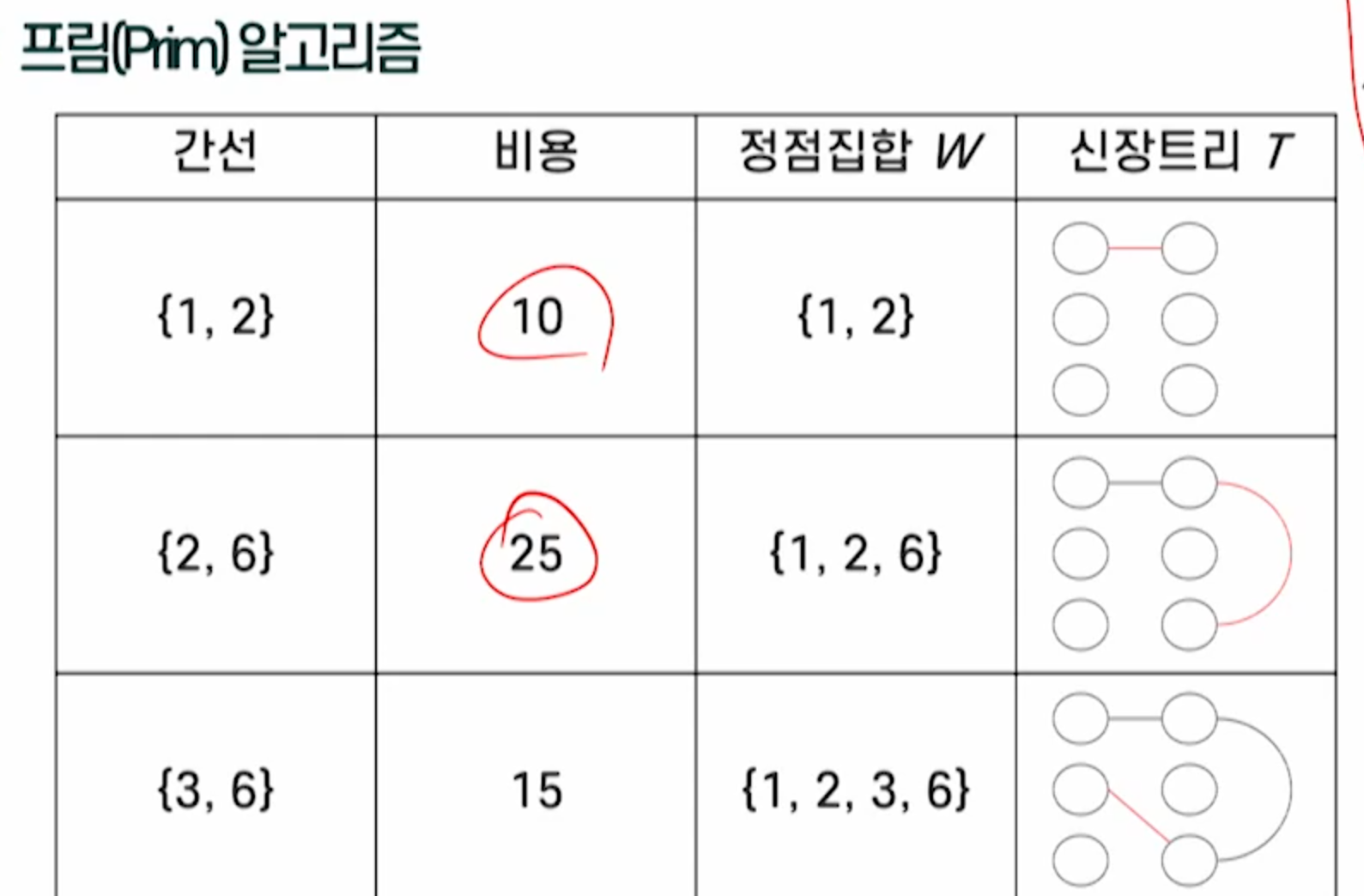
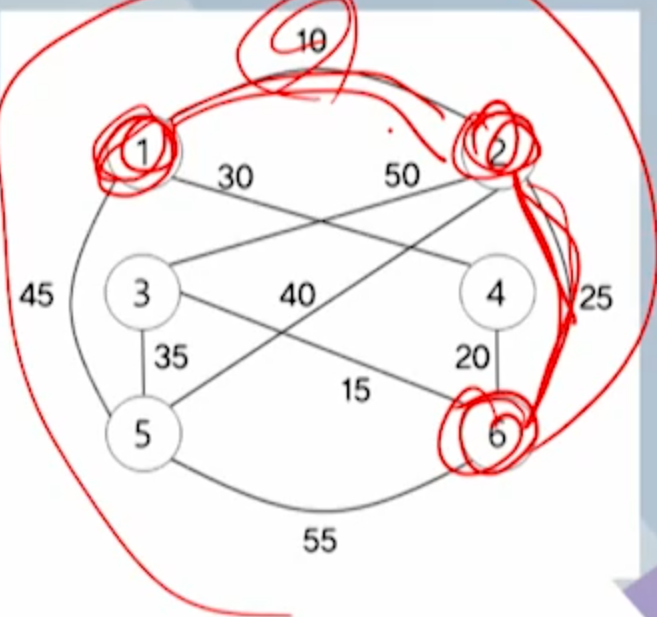
프림 알고리즘
- n개의 정점을 갖는 연결 그래프 G에 대한 최소비용신장트리 T를 구하는 알고리즘
-그래프 전체에서 최소 비용을 갖는 간선{v1,v2}를 선택하여 이 간선을 최소비용신장트리 T에 추가함
- 이 간선을 최소비용신장트리 T에 추가하였을때 사이클을 형성하지않으면 T에추가하고 아니면 무시함
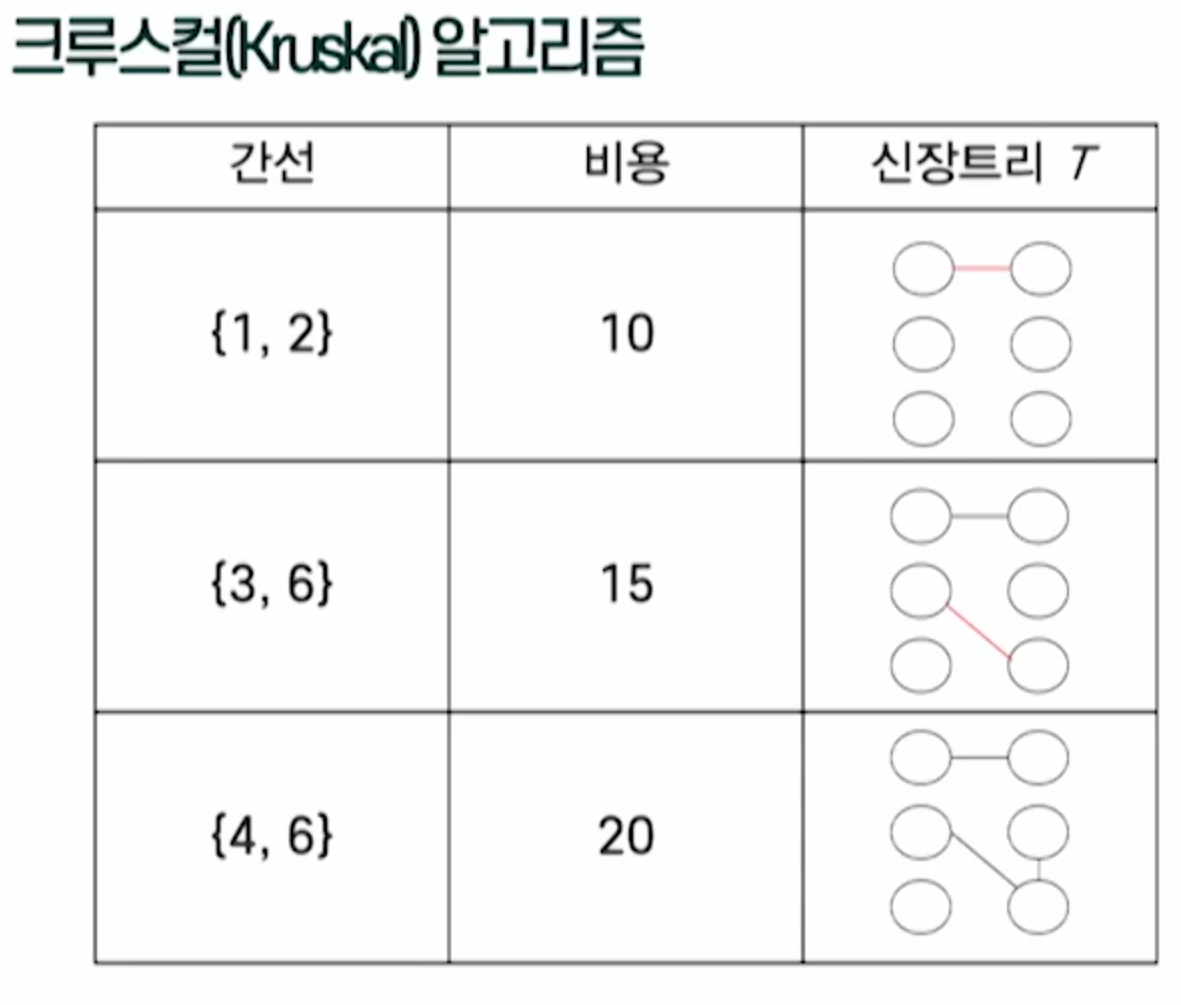
크루스컬 알고리즘
-남은 간선중에서 무조건 최소비용인 간선을 선택한 후 사이클을 형성하지않으면 그 간선을 선택함
- 중간과정에 있는 T는 하나의 트리가 아니고 여러개의 분리된 트리, 즉 숲일 수 있음
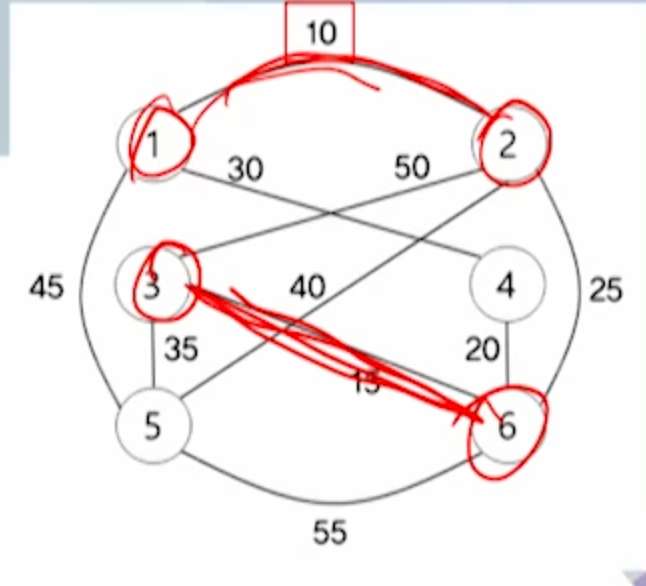
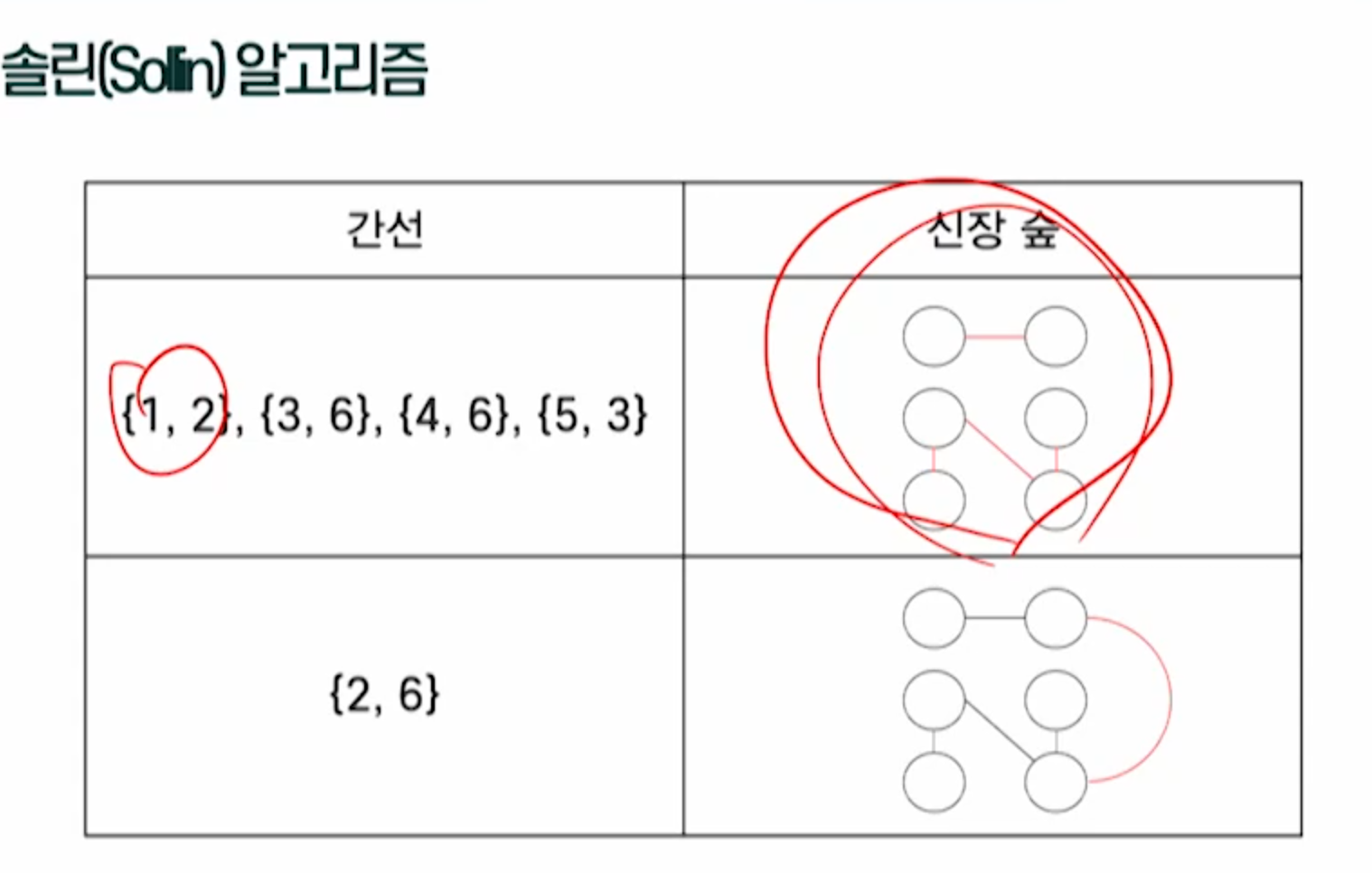
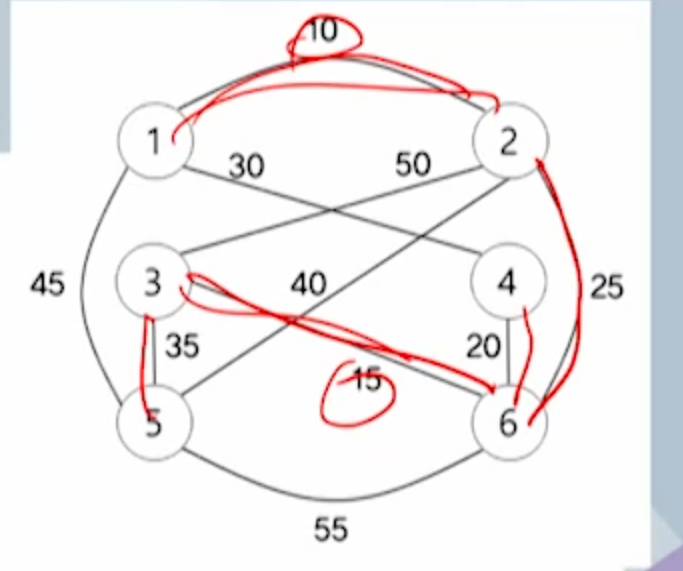
솔린 알고리즘
-간선이 하나도 없는 그래프의 모든 정점으로 구성된 숲에서 시작함
-단계가 거듭되면서 숲 내의 트리들이 최소 비용을 갖는 간선으로 연결
'수업 > 자료구조' 카테고리의 다른 글
| 트리 정리 (1) | 2024.11.17 |
|---|---|
| 12,13 멀티웨이 탐색 트리 (0) | 2024.11.10 |
| 10.선택트리, 숲, 이진트리개수 11.이진탐색트리(BS),Splay,AVL,BB (0) | 2024.11.10 |
| 8. 스레드 트리 9. 우선순위큐, 힙 (0) | 2024.11.09 |
| 7. 트리 (0) | 2024.09.18 |