트리 정리
노드의 차수: 어떤 노드가 가지고 있는 자식노드의 개수
트리의 차수: 트리가 가지고 있는 노드의 차수 중 가장 큰 값
루트의 레벨 : 1
트리의 높이: 트리가 가진 최대 레벨
쓰레드트리
스레드라는 포인터를 갖는 이진트리
스레드 : 정해진 순회 방법에 따른 방문 순서를 유지하는 포인터
오른쪽스레드 : 정해진 순회 순서에 따른 그 노드의 후속노드를 가리킴
왼쪽스레드 : 그 노드의 선행 노드를 가리킴
합병정렬: 차례로 정렬한 데이터 리스트 k개를 완전한 순서를 유지하는 하나의 리스트로 만드는 과정
선택트리 : 합병정렬에 사용하는 특수한트리
히프(Heap) 조건
- 부모노드가 자식노드보다 크거나(최대힙) 작다(최소힙) - (같아도 된다고 한다)
- 완전이진트리이다. 즉 왼쪽부터 노드가 차례대로 채워져야함
히프의 삽입연산
-번호순으로 가장 마지막 위치에 새로운 요소를 삽입하고 부모노드와 비교해가면서 위로 올린다.
-삽입노드가 부모노드보다 크다면 부모노드의 값을 삽입노드위치로 바꾼다. (최대힙)
-그렇게 계속 트리를 올라가다가 삽입노드가 부모노드보다 작다면 해당위치에 삽입할노드 값을 적는다.(최대힙)
히프의 삭제연산
- 맨 마지막노드값을 temp로 저장하고 삭제한다.
-루트노드 (1번인덱스) 자식노드(2번인덱스 ,3번인덱스) 부터 아래로 내려가면서 temp값과 비교한다 (최대힙의 경우)
- temp값이 자식노드중 큰값 보다 더 작다면 자식노드중 큰값을 부모로 올린다 그렇게 아래로 내려가면서 반복한다.
- temp값이 자식노드중 큰값보다 크다면 그 부분이 temp의 적정 위치이므로 해당 부모값에 temp값을 넣어 확정한다.
즉 맨 마지막값을 저장해놓은후 삭제시키고, 맨 마지막값의 위치를 루트노드서부터 아래로 내려오면서 위치를 찾아주는것이다
승자트리
각 노드가 두 자식 노드의 작은 값(승자)인 완전이진 트리
패자트리
각 노드가 두 자식 노드의 큰 값(패자)이며 최종 승자는 0번 노드에 저장하는 완전이진 트리
숲
분리된 트리모임
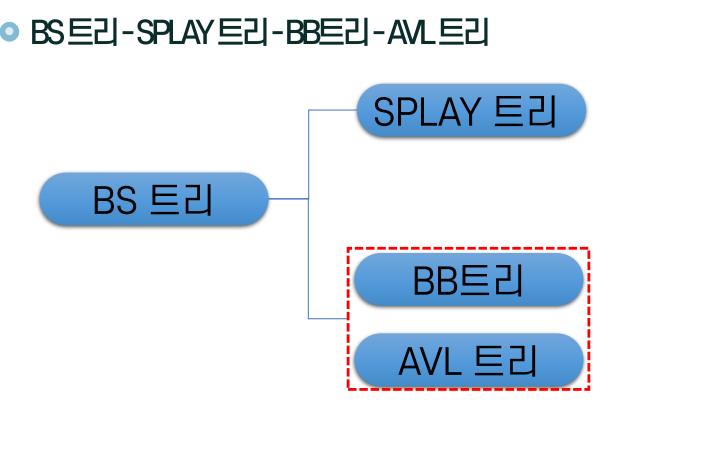
이진탐색트리(BS tree) 조건
-같은 키값을 갖는 노드가 없음
-왼쪽서브트리<루트키< 오른쪽서브트리키
이진탐색트리 삽입연산
-루트부터 아래로 내려가면서 키의 대소관계를 비교하면서 삽입할 key가 존재하는지 검색한다
- 삽입할 key가 없다면(null) 그 위치에 삽입한다
이진탐색트리 삭제 연산
-삭제하려는 노드가 단말노드인경우
삭제하려는 노드를 찾아서 부모노드안의 링크필드를 NULL로 만든다
-삭제하려는 노드가 하나의 왼쪽 이나 오른쪽 서브트리중 하나만 가지고 있는 경우
삭제하려는 노드를 찾아서 삭제하고 서브트리는 자기 노드의 부모노드에 붙여준다.
-삭제하려는 노드가 두개의 서브트리 모두 가지고 있는 경우
왼쪽 서브트리의 가장 오른쪽에있는 노드 or 오른쪽 서브트리의 가장 왼쪽에 있는 노드를 찾는다
여기서는 오른쪽 서브트리의 가장 작은 노드를 사용한다고하면,
삭제하려는 노드를 오른쪽 서브트리의 가장 작은 노드 값으로 바꾸고 삭제하려는 노드위치의 서브트리에서 오른쪽 서 브트리의 가장 작은 값을 삭제시켜준다.
Splay트리
: 자주 탐색하는 키를 가진 노드를 루트에 가깝게 위치하도록 구성한 이진탐색트리
AVL트리
각 노드에서 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차이가 1이하인 이진탐색트리를 말한다.
BB트리
무게가 균형 잡힌 무게균형트리
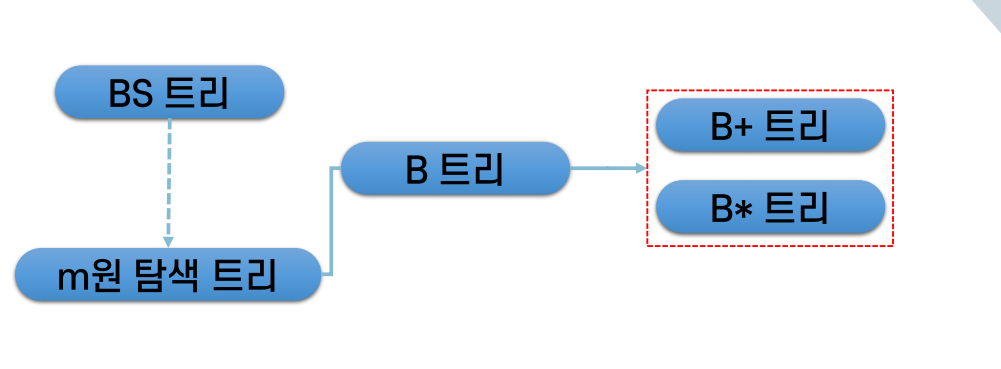
m원탐색트리
: 트리의 노드가 m개 이하의 가지를 가질 수 있는 탐색트리
B트리
: 인덱스 구조를 구현하는 데 가장 일반적으로 사용하는 방법으로 차수가 m 인트리
B*트리
노드의 약 2/3 이상이 차야하는 B트리
B+트리
모든 키값이 잎에 있고 그 키 값에 대응하는 실제 데이터에 대한 주소를 잎노드만이 가지고 있어 인덱스된 순차파일을 구성하는데 사용하는 트리
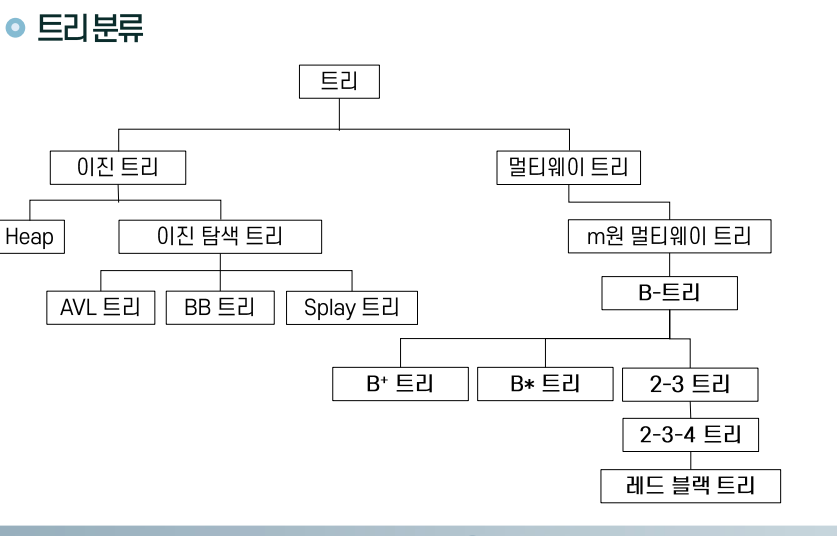
2-3트리
2노드와 3노드만으로 구성한 트리로 B트리 계열과 거의 같은 성능을 유지하면서 상대적으로 삽입삭제가 용이함
왼쪽서브트리에있는 데이터들은 모두 k1보다 작은값이다 중간 서브트리에 있는 값들은 모두 k1보다 크고 k2보다 작다 오른쪽에 있는 데이터들은 모두 k2보다 크다.
2-3-4트리
2-노드,3-노드,및4-노드만으로 구성한 트리로 2-3트리와 같은 특성이 있음
레드블랙트리
:2-3-4트리를 이진트리로 나타낸것으로 기억장소를 효율적으로 사용할 수 있음